Unveiling Ancient Precision: Comparative Metrological Analysis of Predynastic Egyptian Stone Vessels

Imagine a world where ancient artisans carved stone vessels so precisely they rival modern industrial standards - yet no one knows how they did it. For millennia, Predynastic and Early Dynastic Egyptian stone vessels have been enshrined as marvels of craftsmanship, yet archaeologists lack a systematic way to quantify their precision.

This article bridges that gap by applying industrial grade metrology, typically reserved for precision manufacturing, to 51 stone vessels spanning museum collections, private holdings, modern lathe produced vases and modern handmade soft-stone vases.

The debate over these artifacts is no longer theoretical. My own work in this field has been ongoing for two years, and a few weeks ago, Max Fomitchev-Zamilov's published an article that to a wide extent answered a long-standing question: were these vessels shaped by ancient tools of unknown sophistication, or by human hands honed through centuries of practice? His work suggests a conclusive answer, but anomalies persist. For instance, private collection vessels exhibit precision scores 1.7–42× higher than museum or modern handmade counterparts, challenging assumptions about ancient artifacts. Will we find the answer?

This article introduces five distinct metrics to analyze precision:

• Precision Score (Gerdes): A high-value metric that amplifies subtle differences in extreme precision.
• Geometric Continuity Index (Gerdes): A geometrically intuitive measure of continuous surface deviation from ideal form.
• Perpendicular Surface Slice Analysis (Gerdes): A curvature-corrected roundness metric with mathematical equivalence to continuous analysis.
• Quality Score (Fomitchev-Zamilov): A composite score balancing surface smoothness, centering, and consistency through statistically validated components.
• Geometric Mean (Poka, Artifact Foundation): A median-based fusion of circularity and concentricity measurements through geometric mean.

By comparing these frameworks, we uncover how methodological choices - from outlier handling to alignment strategies - reshape conclusions about artifact quality. For example, Geometric Mean is highly sensitive to vessel orientation (a 28% score shift due to rotational alignment), while Geometric Continuity Index excels at creating an intuitively clear surface deviation metric but is less sensitive to fine surface textures.

Ultimately, this work redefines how we evaluate ancient craftsmanship. No single metric reveals the full story - just as no single historian can capture the totality of an era. By synthesizing diverse approaches, we illuminate the interplay between human ingenuity and technological limits, offering a blueprint for future studies in archaeological metrology.

Data provenance and collection methodology:

• Museum vessels (MV): Scans sourced from both Max Fomitchev-Zamilov and Karoly Poka's scanning of vessels from the collection of the Petrie Museum in London. Where overlaps of scanned vessels occur, Fomitchev's datasets are prioritized due to superior interior surface capture and overall scan data quality.
• Handmade vessels (HV): Nine soft-stone vases meticulously crafted using traditional techniques without modern tools. Vases created by Egyptian artisans using methods passed down by generations, obtained specifically for this study by Max Fomitchev-Zamilov and scanned with his Keyence VL-500 3D scanner (10-micron accuracy).
• Industrial reproductions (IV): Nineteen vases produced using modern lathes from both soft and hard stone, primarily scanned by Max with Keyence VL-500 (with IV001-IV003 CT-scanned by Matt Beall for complete interior/exterior analysis).
• Private collection (PV): Scans provided by the Artifact Foundation, including PV001 and PV003 owned by Adam Young (head of the Artifact Foundation) and CT-scanned at Zeiss facilities.

Image courtesy Max Fomitchev-Zamilov's - Photo of museum artifacts from the Petrie Museum

Image courtesy Max Fomitchev-Zamilov's - Photo of Max's collection of handmade Egyptian vases

Image courtesy Max Fomitchev-Zamilov's - Photo of Max's collection of modern stone vases

Image courtesy Artifact Foundation - Photos of Adam Young's collection of Egyptian artifacts

The article strives for a balanced language with the aim of including both technical and non-technical readers alike, while still providing equations and fundamentals necessary for comprehensive understanding and evaluation of the arguments and conclusions set forth herein.

Comparing Precision Measurement Approaches: Five Perspectives on Ancient Craftsmanship

When studying ancient Egyptian stone vessels, how we measure precision matters as much as the measurements themselves. Three different researchers (myself included) have developed unique approaches to quantify the remarkable craftsmanship of these artifacts. Here's a comparative look at their key methods used in this field of study.

To ease the comparison of my proposed Precision Score metric, I have introduced two alternative updates: - The first, Geometric Continuity Index, applies the same methology as the Precision Score, but instead of using the RMD as a baseline, I square the results to get the RMSD instead, making this metric more intuitively comparable with the metrics from the other researchers.
- The second, Perpendicular Surface Slice Analysis, is introduced to ensure the different approach to precision measurement is indeed comparable. The introduced slicing method is similar to what the other researchers have used, but using my distinct method of precision quantification. These methods also employ the direction of lower score = higher precision, making direct comparison with other researchers' methods more intuitive.

All research reports already published on this site included every type of measurement discussed, and the necessary foundations hereof (including measurements from the DG&T standard): Surface deviation analysis, detailed circularity analysis and detailed concentricity analysis - allowing anyone to study these individual components of precision in detail. Refer to the published reports in the catalogue for this data.

The walk-through below only handles the difference of the final quality assessment of each artifact by each researcher.

Precision Score - developed by Stine Gerdes

The Precision Score is uniquely valuable for analyzing the upper limits of ancient manufacturing capabilities, where subtle differences in high-precision work would be indistinguishable using other metrics. It quantifies the exponential increase in difficulty required to achieve progressively higher levels of precision, making it the definitive metric for determining how closely ancient artisans approached industrial-grade accuracy. Higher scores indicate exponentially greater geometric control.

Direction: Higher score = higher precision

Intuition: A specialized metric that magnifies tiny differences in extremely precise work.

Zeiss reference sphere theoretical maximum: 43,943

Calculation Procedure:

1. Generate 2D profile by calculating $\sqrt{x_i^2 + y_i^2}$ from 3D coordinates
2. Fit high-order polynomials (1-5 sections with overlap) to profile
3. Fuse polynomial sections using weighted interpolation at boundaries (infinite weight on boundary points)
4. Calculate $\text{MSD} = \frac{1}{n} \sum (y_i - \hat{y}_i)^2$ (Mean Squared Deviation) for all scan point to composite polynomials
5. Compute Precision Score = $\frac{1}{\text{MSD}}$

Philosophical Foundation: Emphasizes that achieving high precision becomes exponentially more difficult, making linear scales inadequate. The inverse MSD formulation ensures small improvements at high precision levels yield disproportionately higher scores.

Strengths

• Maximum dynamic range (5,122x) enables fine-grained discrimination between high-precision artifacts
• Mathematically reflects reality of precision work through exponential scaling ($\frac{1}{\text{MSD}}$)
• Utilizes full vertex dataset, after removal of damaged parts and areas with insufficient data, with continuous surface analysis (no information loss)

Weaknesses

• Requires logarithmic scaling for visualization due to extreme dynamic range
• Less immediately intuitive than RMSD-based metrics for non-specialist readers

Geometric Continuity Index - developed by Stine Gerdes

Geometric Continuity Index provides the most immediately interpretable measure of geometric fidelity in familiar engineering units (millimeters). It quantifies the average deviation from an idealized smooth surface across the entire artifact, making it particularly valuable for communicating precision levels to both specialist and non-specialist audiences. This metric excels at revealing systematic manufacturing variations across the vessel's complete geometry, with lower values indicating superior control over overall form and surface continuity.

Direction: Lower score = higher precision

Intuition: Measures how closely the vessel's surface matches a mathematically perfect form.

Zeiss reference sphere theoretical minimum: 0.0048

Calculation Procedure:

1. Generate 2D profile by calculating $\sqrt{x_i^2 + y_i^2}$ from 3D coordinates
2. Fit 15th-order polynomials (1-5 sections with overlap) to profile
3. Fuse polynomial sections using weighted interpolation at boundaries (infinite weight on boundary points)
4. Calculate $\text{RMSD} = \sqrt{\frac{1}{n} \sum (y_i - \hat{y}_i)^2}$ between scan data and best-fit surface
5. Report median RMSD across artifact surface

Strengths

• Intuitive physical interpretation (average deviation in millimeters)
• Direct comparability across studies and methodologies
• Clear linear relationship to manufacturing precision (lower = better)
• Robust against implementation variations when using continuous surface analysis

Weaknesses

• Less sensitive to high-precision differences than inverse formulations

Perpendicular Surface Slice Analysis - developed by Stine Gerdes

Perpendicular Surface Slice Analysis serves as the definitive bridge between continuous surface analysis and discrete slice methodologies, demonstrating mathematical equivalence when properly implemented. By collecting all residuals across slices into a single RMSD calculation, it preserves full error distribution while maintaining slice-based analysis framework. This metric is particularly valuable for cross-method validation and for illustrating how curvature-aware slicing eliminates measurement artifacts present in z-axis approaches. Lower Perpendicular Surface Slice Analysis scores indicate better overall roundness control when accounting for surface geometry.

Direction: Lower score = higher precision

Intuition: Measures roundness of the vessel by slicing through perpendiculars to its surface.

Calculation Procedure:

1. Generate 2D profile by calculating $\sqrt{x_i^2 + y_i^2}$ from 3D coordinates
2. Slice artifact perpendicular to surface normal (0.2mm thickness, 0.2mm spacing)
3. For each slice:
1. Calculate median distance from z-axis to points (|median_x|)
2. Find tangent line at [$\text{median}_\text{distance}, \text{median}_y$] using polynomial derivative
3. Compute perpendicular distances from all slice points to tangent line (residuals)
4. Collect ALL residuals from ALL slices into one dataset
5. Calculate RMSD = $\sqrt{\frac{1}{N} \sum (\text{residual}_i)^2}$ where $N = $ total number of points across all slices

Strengths

• Mathematical equivalence to Geometric Continuity Index (providing critical methodological bridge)
• Explicit curvature correction by slicing perpendicular to surface normal
• Eliminates distortion artifacts inherent in z-axis slicing methods
• Direct comparison pathway to slice-based methodologies

Weaknesses

• Sensitive to vertex density in low-resolution scans
• Less sensitive to high-precision differences than inverse formulations

Quality Score - developed by Max Fomitchev-Zamilov

Quality Score excels at diagnosing specific manufacturing issues by separating concentricity errors from surface roughness and measuring consistency. It is particularly valuable for identifying systematic alignment problems during production, with lower scores indicating better overall control of both circularity and rotational consistency. This metric reveals how artisans maintained precision throughout the manufacturing process, with each component ($\text{RMSD}$, $\Delta C$, $\sigma(\Delta C)$) providing distinct insights into different aspects of craftsmanship quality.

Direction: Lower score = higher precision

Intuition: Combines three aspects of quality: surface smoothness, centering accuracy, and consistency.

Zeiss reference sphere theoretical minimum: 1.1

Calculation Procedure:

1. Intersect 3D mesh with parallel planes (z-axis orientation)
2. For each slice (100 total, excluding top/bottom 2.54mm):
1. Fit circle using least squares
2. Calculate $\text{RMSD}$ (RMS error of fit)
3. Compute concentricity,
   initially defined as: $\Delta C = \sqrt{x_c^2 + y_c^2}$
   later revised to: $\Delta C = \sqrt{(x_c- \langle x_c \rangle )^2 + (y_c - \langle y_c \rangle )^2}$
3. Apply statistical filtering: exclude slices where:
   $\Delta C - \langle \Delta C \rangle > 2 \langle \Delta C \rangle$ or $\text{RMSD} - \langle \text{RMSD} \rangle > 2 \langle \text{RMSD} \rangle$
4. Calculate composite quality score: $Q = \langle \text{RMSD} \rangle + \langle \Delta C \rangle + \sigma(\Delta C)$

Strengths

• Error type separation ($\text{RMSD}$, $\Delta C$, $\sigma(\Delta C)$ reveal distinct manufacturing aspects)
• Statistical robustness through outlier slice filtering
• Polygonally-based mesh/plane intersection avoids curvature distortion artifacts

Weaknesses

• Fixed slice count (100) may not optimally sample all vessel sizes

Geometric Mean - developed by Karoly Poka (Artifact Foundation)

Direction: Lower score = higher precision

Intuition: None. Represents a mathematical chimera - dimensionally consistent but geometrically meaningless

Zeiss reference sphere theoretical minimum: 0.0065

Calculation Procedure:

1. Slice artifact in z-plane (slice height not fixed, between 0.03mm-0.27mm thickness)
2. For each slice:
   1. Fit circle using least squares
   2. Calculate circularity error (RMSD of fit)
   3. Compute concentricity ΔC = $\sqrt{x_c^2 + y_c^2}$
3. Determine median circularity and median concentricity
4. Calculate composite score: $\sqrt{\text{circularity}_{median} \times \text{concentricity}_{median}}$

Weaknesses & Rejection

1. Foundational Mathematical Flaws
   1. Dimensional Incompatibility and Lack of Geometric Meaning
      This metric combines two dimensionally incompatible quantities without justification. While the final unit appears consistent (length), the intermediate product has no physical meaning in geometric precision assessment.
      
      The name of the metric Geometric Mean, does not refer to any geometrical properties of the artifact: The term Geometric Mean refers to the name of the applied function $\sqrt{a \cdot b}$.
      
      This differs fundamentally from valid metrics:
      • Geometric Continuity Index: Directly measures deviation magnitude ($\sqrt{1/n\sum(y_i-\hat{y}_i)^2}$)
      • Precision Score: Inverse of squared error ($1/MSD$), reflecting precision difficulty
      • Quality Score: Sum of meaningful components ($RMSD + ΔC + \sigma(ΔC)$)
   
   
   2. Violation of Error Propagation Principles
      Precision metrics must adhere to error propagation principles, however this approach violates fundamental statistical requirements:
      
      Error Sensitivity Analysis: $$dQ = \frac{1}{2\sqrt{c \cdot ΔC}} \cdot (ΔC \cdot dc + c \cdot dΔC)$$ Differential equation of Geometric Mean metric where
      • c: Circularity RMSD median (in mm, measures surface roughness)
      • ΔC: Concentricity median (in mm, measures center alignment)
      
      This reveals disproportionate sensitivity where either component approaches zero, creating artificial precision "cliffs" with no physical basis, artificially increasing the Geometric Mean calculation. This mathematical flaw fundamentally undermines any archaeological conclusions, as it misrepresents the true relationship between different precision levels in ancient manufacturing.
      
      Contrast with Valid Metrics:
      • Geometric Continuity Index: Linear error propagation ($dRMSD \propto d\varepsilon$)
      • Precision Score: Exponential sensitivity reflecting manufacturing reality ($dPS \propto 1/RMSD^3$)
      • Quality Score: Additive components with clear physical interpretations
      
      
      
2. Statistical Misapplication and Data Distortion
   1. Catastrophic Misapplication of Statistical Concepts - The Median Selection
      The use of medians for both equation components represents a fundamental statistical misunderstanding.
      
      The Median Fallacy
      The erroneous belief that "median makes results robust" ignores that:
      • Precision assessment requires full error distribution
      • Manufacturing quality depends on worst-case deviations, not central tendency
      • Medians hide systematic manufacturing variations critical to analysis
      
      For precision measurement, we require metrics sensitive to the tail of the error distribution. The Geometric Mean approach is mathematically equivalent to: $$ \text{Geometric Mean} \propto \left(F^{-1}(0.5)\right)^2 $$ Median Definition in Statistical Terms:
      • For any error distribution, the median = $F^{-1}(0.5)$
      • Where $F(x) = P(X \leq x)$ is the error cumulative distribution function (probability that error $X$ is less than or equal to $x$)
      
      This focuses exclusively on the 50th percentile, ignoring the critical 90th+ percentile errors that determine manufacturing quality.
      
      Statistical Consequences
      • Discards 50% of error information (all values above median)
      • Artificially suppresses manufacturing variations critical to precision assessment
      • Creates false precision by ignoring systematic deviations
      
      Precision Manufacturing Requirement
      True precision requires control over:
      • Not just the central tendency (median)
      • But the entire error distribution
      • Particularly the upper tail ($ F^{-1}(0.9) $ and beyond)
      
      This is why industrial metrology standards (ISO 1101, ASME Y14.5) focus on maximum deviations rather than medians.
      
      Contrast with Quality Score which correctly uses:
      • $\langle RMSD \rangle$: Mean RMS error (captures overall surface quality)
      • $\langle ΔC \rangle$: Mean concentricity (systematic alignment)
      • $\sigma(ΔC)$: Standard deviation (consistency of alignment)
      
      This preserves the full error distribution while separating meaningful components.
      
      
3. Geometric Implementation Errors
   1. Curvature Distortion in Slicing

      The z-axis parallel slicing, with documented variations between 0.003mm-0.27mm in slice height, introduces geometric distortion that potentially distorts measurements.

      Mathematical Proof:
      For a vessel with radius $ R $ and curvature $ \kappa $, the distortion error $ \varepsilon $ introduced by z-slicing is:

      $$ \varepsilon \approx \frac{\kappa \cdot h^2}{2} $$

      Where $ h = $ slice height.

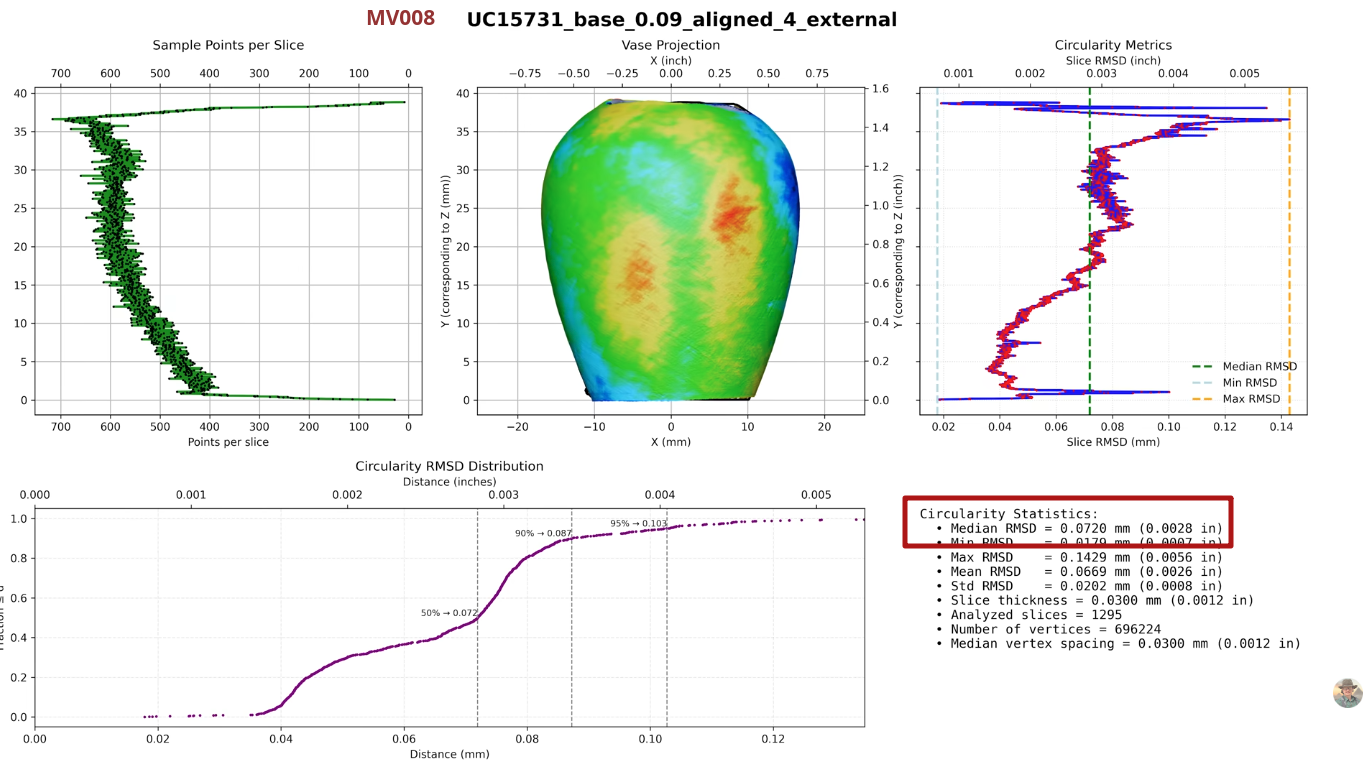
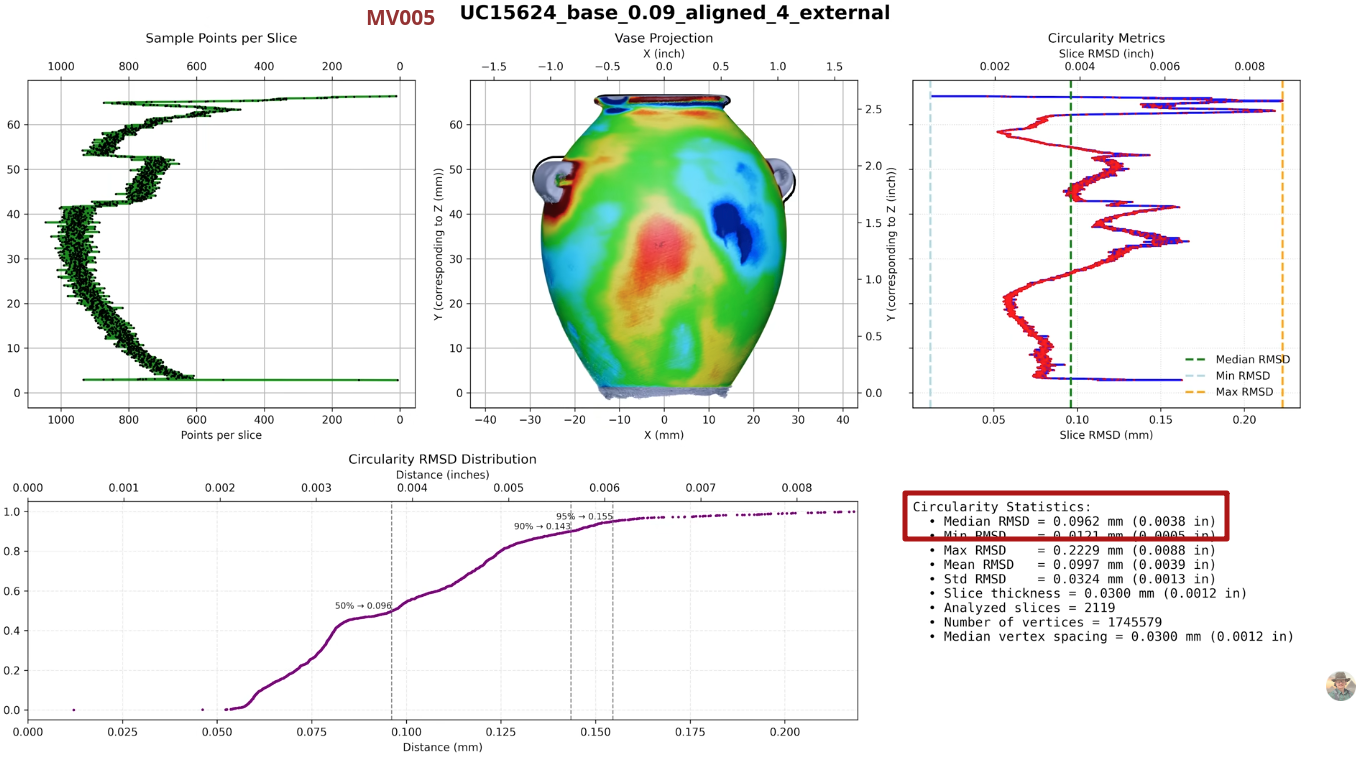
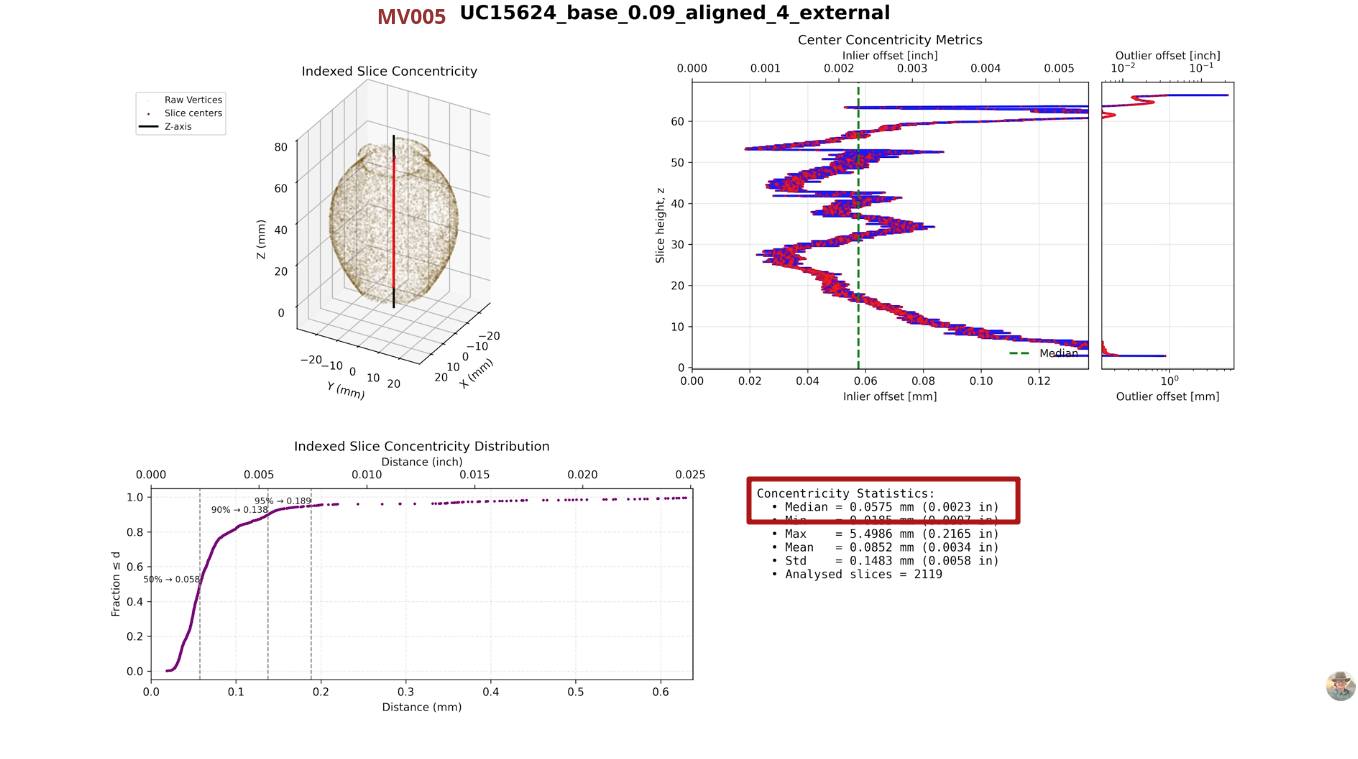
      Let's take the vessel MV005 (UC15624) as an example:
      Calculating Geometric Mean with slice-height 0.003 gives us:
      Result: 0.0543 (Fit RMSD Median: 0.0867, Concentricity Median: 0.0340)
      
      Calculating Geometric Mean with slice-height 0.27 gives us:
      Result: 0.0554 (Fit RMSD Median: 0.0982, Concentricity Median: 0.0313)
      
      The result decreases 2%, and median RMSD error increases significantly 13%. This variation will irregularly affect vessels differently depending on their shape.

      Contrast with Perpendicular Surface Slice Analysis:

      • Slicing perpendicular to surface normal
      • Using tangent line reference at each slice
      • Ensuring measurements reflect true geometry
      • Quality Score method eliminates this distortion by:
        • Intersecting the 3D mesh with parallel planes (z-axis orientation)

      Critical Consequence:

      • Vessels measured with thinner slices (0.003mm) show artificially improved precision
      • Creates false ranking where measurement protocol determines score
      • Violates fundamental requirement for standardized metrology

4. Methodological Inconsistencies and Errors
   1. Calculation Errors Reveal Fundamental Flaws
      Documented calculation error for MV013:
      Looking at the presentation of the research results, the artifact MV013 (UC41053) falls into the top 5 precision vessels. However, a critical error presents itself. The median RMSD fit error is documented at 0.14mm and the median concentricity error at 0.49mm, let's do the math: $$ \sqrt{0.14 \times 0.49} = 0.262 \quad (\text{correct}) \\ \text{Reported as: } 0.128 \quad (\text{error}) $$ This 51% underestimation reveals:
      
      1. Poor quality control: No validation of calculations
      2. Method weakness: Errors like this should not be introduced with consistent code structure and output reporting.
      3. Potential data manipulation: Data manipulation has been noted before in presentations by the Artifact Foundation.
      
      
   2. Alignment Sensitivity Analysis
      The Geometric Mean metric shows extreme sensitivity to alignment.
      
      Mathematical Proof:
      For a vessel with true concentricity $ \Delta C_{\text{true}} $, misalignment of $ \delta $ causes: $$ \Delta C_{\text{measured}} = \sqrt{\Delta C_{\text{true}}^2 + \delta^2 + 2 \cdot \Delta C_{\text{true}} \cdot \delta \cdot \cos\theta} \\ Q = \sqrt{c \times \sqrt{\Delta C_{\text{true}}^2 + \delta^2 + 2 \cdot \Delta C_{\text{true}} \cdot \delta \cdot \cos\theta}} $$ Creating a non-linear amplification of alignment errors. Measurements show that the alignment strategies employed by ArcSci outperform the alignment strategy employed by Artifact Foundation when using their own metric.
      
      Let's explore this critical failure mode, by going through some examples:
      ArcSci applied top and bottom margin of 4mm, slice height of 0.05mm.
      Artifact Foundation applied unknown top and bottom margin, slice height of 0.03mm.
      
      MV008 (UC15731)
      • ArcSci results:
        Geometric Mean: 0.047 | RMSD median: 0.073 | ΔC median: 0.0304
      Vessel rotated 0.05° to the right, away from proposed optimal alignment:
      Geometric Mean: 0.039 | RMSD median: 0.073 | ΔC median: 0.0212
      • Artifact Foundation results:
        Quality Score: 0.062 | RMSD Median: 0.072 | ΔC median: 0.0536
      
      MV005 (UC15624)
      • ArcSci results:
        Geometric Mean: 0.052 | RMSD median: 0.09 | ΔC median: 0.031
      • Artifact Foundation results:
        Geometric Mean: 0.074 | RMSD median: 0.096 | ΔC median: 0.0575

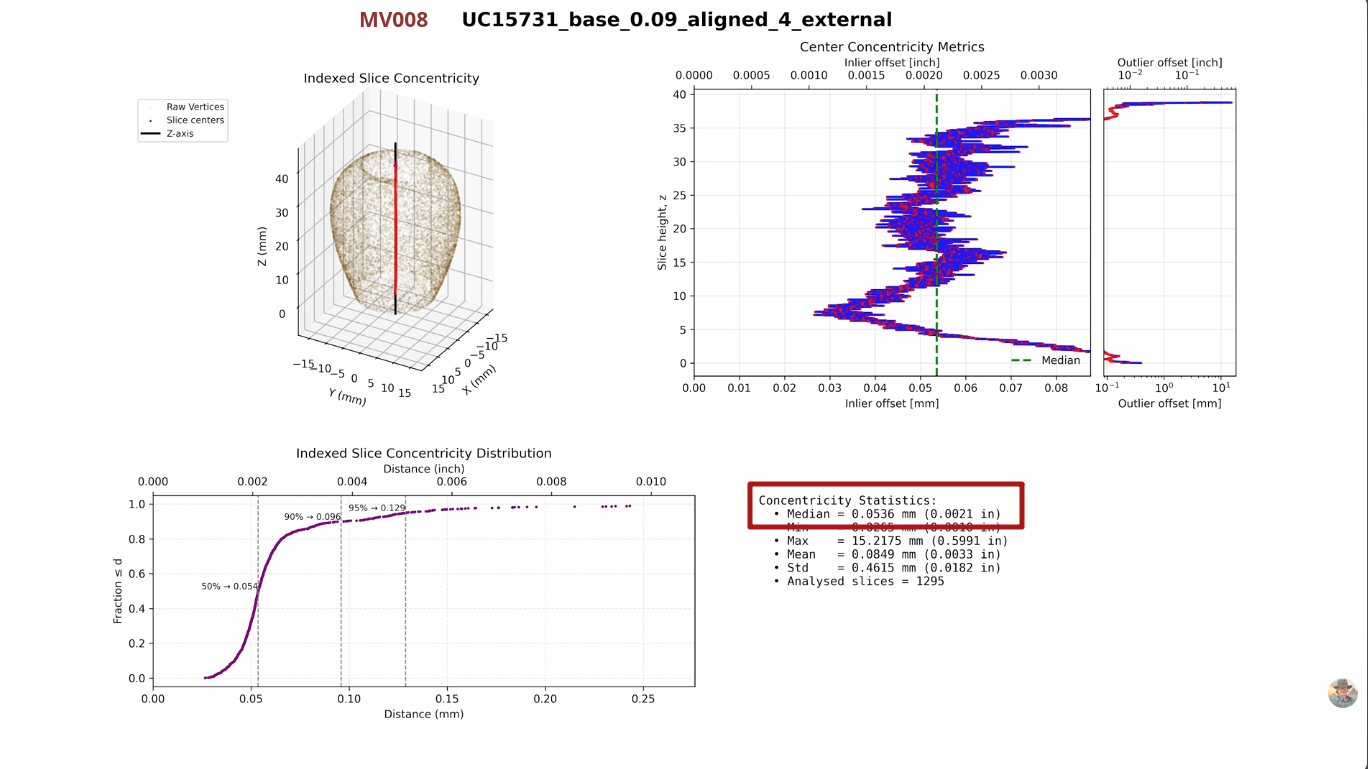
      Shifting the rotation of the artifact MV008 a mere 0.05° to the right improved the Geometric Mean score by 17%.

      In reality, this means that the final output of the Geometric Mean metric can be artificially manipulated, by modifying the artifact alignment in miniscule and almost undetectable increments.

Conclusion: Artifact Foundations Geometric Mean Methodology is Fundamentally Invalid
The approach represents a catastrophic failure in precision metrology for three fundamental reasons:

1. Complete Lack of Theoretical Foundation: The methodology behind Geometric Mean score suffers from critical theoretical deficiencies:
   • No stated purpose: Fails to articulate what aspect of precision is being measured
   • No error analysis: Ignores fundamental metrology principles
2. Mathematical Invalidity: Combines geometrically incompatible quantities without justification, creating a metric that lacks physical meaning
3. Statistical Misapplication: Uses medians to artificially improve scores while discarding critical manufacturing variation data, violating basic principles of precision measurement

The documented lack of theoretical foundation confirm this methodology's unsuitability for archaeological precision analysis. In contrast all other analyzed metrics represent valid theoretically grounded approaches that:

• Capture meaningful aspects of manufacturing precision
• Maintain geometric and statistical integrity
• Support archaeological interpretation through rigorous metrology

Artifact Foundation's methodology should be rejected as fundamentally flawed and scientifically invalid within the research domain of precision analysis for ancient Egyptian vessels. It's continued use would produce misleading results that obscure rather than reveal the true manufacturing capabilities of ancient artisans.

Final Notes
The theatrical dismissal of my own methodologies by Artifact Foundation, based solely on them not having access to implementation source-code, fundamentally misrepresents scientific replication standards.

Legitimate replication requires methodological transparency - sufficient procedural detail to reproduce results - not code submission. Karoly Poka's conflation of open-source mandates with peer review reveals a critical misunderstanding of scientific epistemology: Validation occurs through independent implementation of described methods, not access to proprietary implementations.

This error exemplifies his broader pattern of substituting procedural gatekeeping for substantive critique, further undermining his credibility in precision metrology - or any kind of scientific endeavor.

True scientific discourse demands engagement with methodological validity, as rigorously demonstrated in this analysis - not diversionary demands irrelevant to empirical verification.

When scientists rigorously test each other's methods - not by demanding code and performing theatrics, but by implementing documented procedures - they advance knowledge together. Poka's avoidance of this core scientific practice exposes his critique as performative, not probative.

Comparison conclusion

These five metrics form a complementary framework for analyzing ancient vessel precision:

• Precision Score for maximum discrimination at high precision levels
• Geometric Continuity Index for intuitive interpretation of overall geometric fidelity
• Perpendicular Surface Slice Analysis for methodological bridging between continuous and slice-based approaches - as this metric was solely created for this purpose, it will not be used in future analysis
• Quality Score for diagnosing specific manufacturing aspects through error component separation
• Geometric Mean - rejected

Comparative Summary
This comparison reveals a crucial insight: no single metric tells the complete story of ancient craftsmanship. Each approach illuminates different aspects of manufacturing quality, much like how multiple witnesses might describe the same event from different perspectives. By using several complementary methods, researchers can develop a more nuanced understanding of both the technical capabilities of ancient Egyptian artisans and the specific challenges they faced in creating these remarkable stone vessels. The most revealing analyses come not from choosing one "best" method, but from understanding what each approach uniquely contributes to our interpretation of ancient manufacturing excellence.

Empirical Validation: Museum Vessels Align with Handmade Craftsmanship, Private Collections Defy Industrial Benchmarks

This section resolves the central archaeological debate through visualized metrological evidence. By plotting exterior versus interior precision scores across all 51 artifacts - spanning museum collections, private holdings, modern lathe-produced vases, and contemporary handmade examples - we confirm Max Fomitchev-Zamilov's hypothesis: museum-held Predynastic vessels exhibit precision indistinguishable from verifiably modern handmade vases.

Methodological Transparency for Cross-Validation

To ensure rigorous comparative analysis, we established standardized protocols where prior methodologies lacked clarity:

For the implementation of Geometric Mean metric

• Slice optimization: Slice heights dynamically adjusted to 0.005–0.2mm based on scan density (may inflict distortion from vessel curvature).
• Edge exclusion: Fixed 4mm top/bottom margins prevent distortion from flat surfaces of top and bottom.
• Data integrity: Slices with <60 points discarded - critical for geometric validity but absent in defining protocol.
• Alignment superiority: The curvature-corrected axis alignment used by ArcSci significantly reduced concentricity median errors for artifacts (example: Artifact MV005, 0.031 vs. 0.0575, reduced by 46%), explaining why the ArcSci implementation of Geometric Mean generally produce a lower score than the results published by Artifact Foundation.
• Alignment sensetivity: Concentricity measurements proved particularly sensitive to even minute rotational adjustments of the artifact (a 0.05° shift can alter concentricity median values by 30% (0.0304mm before, 0.0212mm after), as demonstrated in MV008 analysis), whereas circle fit error (RMSD) remains relatively stable under the same conditions.

For the implementation of Quality Score

• Slice optimization: Slice heights fixed at 0.2mm (the Python implementation handles both vertex slicing and mesh interpolation - both method gives very similar results)
• Alignment variations: Fomitchev and I aligned vessel scans independently, which will introduce slight differences in the results.

Comparison of Quality Metric Implementation, Max Fomitchev-Zamilov vs. Current Study:

The following table presents a direct comparison between my implementation of Max Fomitchev-Zamilov's Quality Metric and the results provided by Max himself for specific museum artifacts. This comparison reveals important insights about methodological implementation differences that affect final precision assessments.

Key Observations

This comparison highlights the critical importance of methodological transparency in archaeological metrology. While our implementations differ in specific calculations, the fundamental conclusion remains unchanged: museum-held Predynastic vessels exhibit precision indistinguishable from modern handmade vases. I look forward to discussing these implementation differences with Max to establish a fully standardized approach for future research.

To ensure methodological consistency across this study, all circle fitting employed the scikit-image CircleModel implementation (a well-established scientific Python module).

Critical Data Refinements

To isolate authentic manufacturing signatures, we implemented targeted exclusions:

• Elliptical Petrie Museum vessels (previously documented in this article) were removed as outliers, as their non-circular profiles would artificially distance the MV group from handmade counterparts.
• The industrially made vessel IV019 will be excluded from the data-set due to it's high interior precision made by a drill (no curvature on the interior cavity).
• Extreme outliers excluded from distribution center calculations:
  • Museum vessels MV011 and MV013 (all metrics)
  • Handmade HV003 and HV004 (Quality Score)
  • Handmade HV003 (Geometric Mean)
  • Industrial lathe vases IV019 (all metrics)

These exclusions ensure distributions reflect typical craftsmanship rather than pathological edge cases.

Validation Framework

The resulting precision maps (Figures 1–4) reveal four statistically distinct clusters corresponding to artifact categories:

• PV: Private collection hard stone artifacts (hard stone)
• MV: Petrie Museum hard stone vases (hard stone)
• HV: Handmade modern Egyptian vases (soft stone)
• IV: Industrial lathe produces vases (soft and hard stone)

Critically, the convergence of MV and HV distributions across multiple metrics confirms that museum-held Predynastic vessels operate within the precision limits of rudimentary hand-guided tools. Conversely, PV specimens consistently achieve scores 1.7–42× higher than museum or handmade artifacts - exceeding even industrial benchmarks in some cases. This anomaly demands rigorous scrutiny of provenance, though definitive attribution requires methodologies beyond current scope.

Understanding Our Statistical Evidence - Quantifying How Much Each Vessel Category May Belong to the Same Group

These statistical tools work together like different lenses: The Mann-Whitney test tells us if differences are likely real, effect size reveals how meaningful those differences are, and superiority ratios quantify how much better one group performs. Together, they provide a complete picture that goes beyond simple "better/worse" comparisons to reveal the nuanced reality of ancient craftsmanship, confirming museum artifacts as achievements of a hand-guided manufacturing process, while highlighting extraordinary anomalies in private collections that demand further investigation.

To ensure our findings stand on solid scientific ground, we employed several statistical tests to analyze the precision data. Here's what these technical terms mean for our understanding of ancient craftsmanship, with real data from our study.

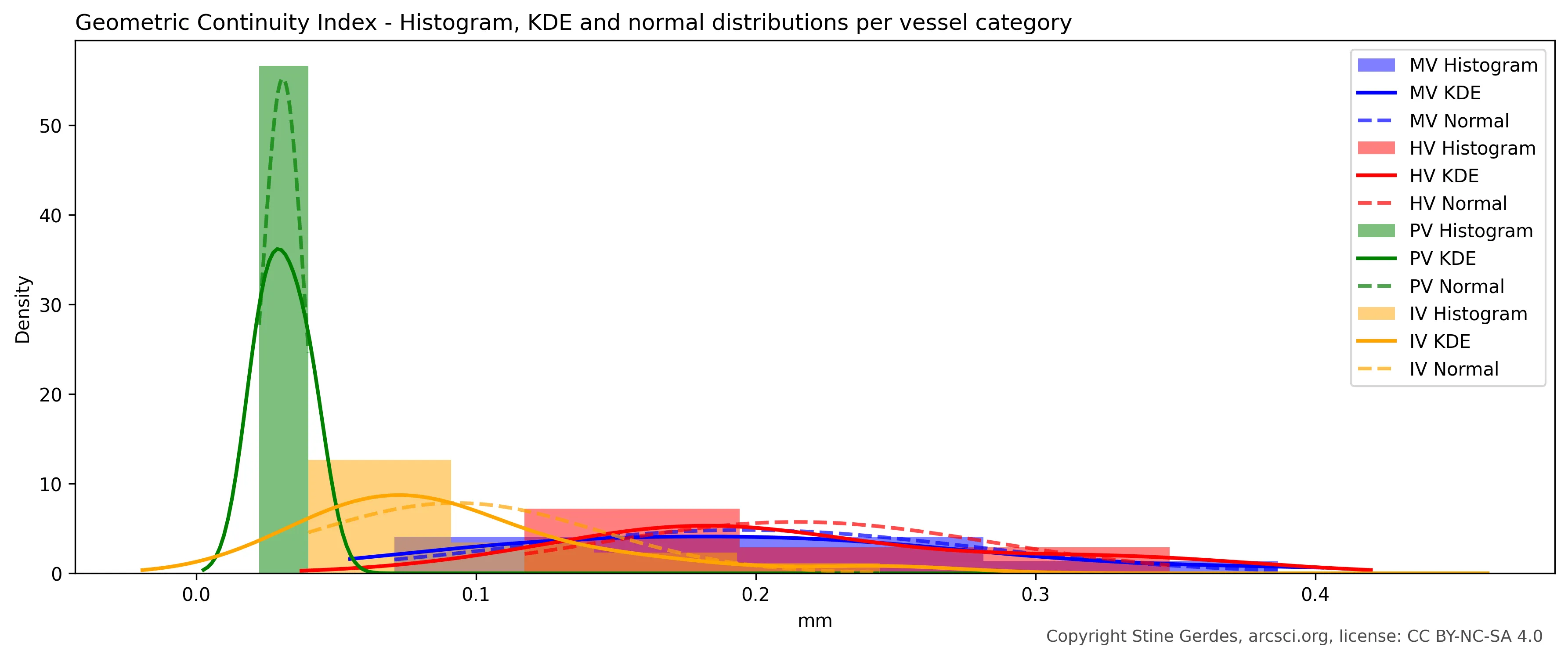Histogram of Geometric Continuity Index for MV, HV, PV and IV categories

Mann-Whitney U Test: The "Real Difference" Detector

Imagine comparing two jars of marbles-one from museum artifacts, one from handmade reproductions. If you mixed them together and couldn't tell which came from which jar, the difference might be random. The Mann-Whitney U test answers: "How likely is it that these two groups actually come from different manufacturing processes?"

• What it tells us: Whether the precision differences between groups (like museum vs. handmade) are likely real or just random variation
• How to read it: A p-value below 0.05 means there's less than a 5% chance the observed difference happened by random chance alone
• In our study: When comparing museum (MV) and handmade (HV) artifacts, most metrics showed p-values above 0.05, confirming these groups are non-separable, and operate within the same hand-guided precision limits

Mann-Whitney U Test between category "MV" and "HV"

How to read our actual data: For most metrics, the p-values for exterior surfaces are well above 0.05 (like 0.6366 for Precision Score), meaning there's a 63.66% chance the observed differences between museum and handmade artifacts occurred randomly - too high to conclude they represent different manufacturing processes. The only exception is Geometric Mean for interior surfaces (p=0.0434), which dips just below the 0.05 threshold, again demonstrating the unreliability of this metric.

Interestingly, while the combined Quality Score analysis shows statistical significance (p=0.0242), neither the exterior (p=0.0667) nor interior (p=0.2614) surfaces individually reach significance. This pattern suggests that while there may be subtle differences between museum and handmade artifacts when considering both surfaces together, these differences aren't consistently apparent when examining surfaces separately - a nuance that reinforces our conclusion that both groups operate within the same fundamental precision framework.

This overall pattern confirms that museum-held Predynastic vessels consistently align with hand-guided craftsmanship and use of rudimentary tools across all four of the validated metrics, with only minor, surface-specific variations that reflect natural manufacturing nuances rather than fundamentally different production methods.

Mann-Whitney U Test between category "MV" and "IV"

What the MV/IV comparison reveals: When we compare museum artifacts to industrial benchmarks, the story changes dramatically. For exterior surfaces, all metrics show extremely low p-values (as low as 0.0003), meaning there's less than a 0.07% chance these differences occurred randomly - virtually confirming they represent fundamentally different manufacturing processes. This is exactly what we'd expect: handcrafted ancient artifacts should be less precise than modern machine-made objects.

The interior surfaces show more nuanced results, with some metrics (like Quality Score) still showing highly significant differences (p=0.0050), while others approach or exceed the threshold of statistical significance.

Cohen's d Effect Size: The "How Big is the Difference?" Measure

Statistical significance tells us if a difference exists, but effect size tells us how meaningful that difference is. Imagine two bakers-one makes loaves 1cm taller than the other. Statistically, this might be significant with enough measurements, but practically, it doesn't matter for your sandwich.

• What it tells us: The practical importance of differences between groups, measured in standard deviation units
• How to read it:
• Small effect (|d| < 0.5): A statistically detectable difference that may not matter practically
• Medium effect (0.5 ≤ |d| < 0.8): A clear, noticeable difference
• Large effect (|d| ≥ 0.8): A substantial, meaningful difference
• In our study: The large effect size in Geometric Mean for interior surfaces revealed a meaningful pattern related to ancient manufacturing techniques, while small effects between MV and HV in other metrics confirmed their practical similarity

Cohen's d Effect Size between category "MV" and "HV"

How to read our actual data: For exterior surfaces, three of five metrics show small effect sizes below 0.5, confirming that museum and handmade artifacts operate within the same practical precision range. The Precision Score shows a medium effect (0.44), while Quality Score surprisingly shows a large effect (1.09) despite non-significant p-values - highlighting how effect size and statistical significance provide complementary insights.

The interior surfaces tell a more nuanced story: All metrics except Quality Score show large effects (0.86-1.14), indicating museum artisans achieved significantly better interior precision. Geometric Mean shows the largest effect size (1.14), confirming its particular sensitivity to axis alignment differences between groups - although it should be kept in mind that the Geometric Mean metric is fundamentally invalid, and only included here in the interest of comparison and statistical illustration.

Cohen's d Effect Size between category "MV" and "IV"

What the MV/IV effect sizes reveal: The effect sizes between museum and industrial artifacts tell a powerful story about manufacturing capabilities across time. For exterior surfaces, all metrics show large effect sizes (1.12-1.57), confirming that ancient handcrafted vessels fall significantly short of modern machine precision - a difference of more than one standard deviation in every measurement system.

The interior surfaces present a fascinating contrast: while three metrics show medium effects (0.66-0.77), suggesting ancient artisans achieved results closer to modern machinery than expected for this challenging aspect of vessel production, two metrics tell a different story. Quality Score maintains a large effect (1.19), and Geometric Mean shows an exceptionally large effect (1.89) - nearly two standard deviations difference.

The Geometric Mean's extreme interior effect size requires special explanation. Unlike other metrics, this measurement is extremely sensitive to axis alignment consistency. Our previous analysis documented that Predynastic artisans typically repositioned vessels once during exterior shaping (creating two slightly different axes visible around mid-vessel height), while maintaining consistent alignment when working the cavity of the interior surfaces. Since interior scans only capture the lower portion of vessels where no repositioning occurred, this creates artificially low $concentricity_{median}$ values in Geometric Mean - magnifying the precision difference between ancient and industrial artifacts specifically for interior surfaces. This mathematical amplification effect explains why Geometric Mean shows such an extreme interior effect size compared to other metrics that don't emphasize axis continuity to the same degree.

Superiority Ratio: The "How Much Better?" Comparison

When private collection specimens appeared more precise than industrial benchmarks, we needed a straightforward way to quantify this difference - not just whether it existed, but by how much.

• What it tells us: How many times more precise one group is compared to another (with direction depending on the metric)
• How to read it:
• For Precision Score (higher=better): Ratio > 1 means PV is better
• For other metrics (lower=better): Ratio < 1 means PV is better
• Values far from 1 indicate substantial differences
• In our study: Private collection specimens showed ratios indicating extraordinary precision that surpasses industrial benchmarks across multiple metrics - statistically improbable for genuine ancient artifacts

Superiority Ratio between category "PV" and "IV"

How to read our actual data: For metrics where lower values indicate better precision (Geometric Continuity Index, Perpendicular Surface Slice Analysis, Quality Score, and Geometric Mean), ratios significantly below 1 reveal how much more precise private collection specimens are compared to industrial benchmarks. The most striking finding is for exterior surfaces: Private collection specimens achieve 48× better precision than industrial benchmarks in Geometric Continuity Index (1/0.0208 = 48.1) and 24× better in Perpendicular Surface Slice Analysis (1/0.0417 = 24.0).

For Precision Score which works in the opposite direction (higher values indicate better precision), we interpret the ratio differently. Since Precision Score ratios are below 1, this means industrial artifacts achieve higher Precision Scores than private collection specimens. To quantify this difference: for interior surfaces, industrial artifacts show 1.55× better precision than private collection specimens (1/0.6458 = 1.55), while for exterior surfaces the difference is nearly negligible (industrial artifacts are only 1.02× better). This counterintuitive finding reveals an important nuance: while private collection specimens achieve extraordinary smoothness and roundness (captured by other metrics), they lack the consistent, uniform precision across the entire surface that gives industrial artifacts their edge in the Precision Score metric.

These complementary perspectives create a complete picture: private collection specimens show 2.8× better precision in smoothness and roundness metrics, while industrial artifacts achieve slightly better consistency across surfaces (captured by Precision Score). This extraordinary combination of properties - unprecedented smoothness with slightly less surface consistency - creates an insurmountable statistical case that private collection specimens operate outside known manufacturing paradigms for ancient artifacts, anomalies that require careful provenance verification.

Visualizing Precision: Five Perspectives on Ancient Craftsmanship

The four primary precision metrics (Precision Score, Geometric Continuity Index, Perpendicular Surface Slice Analysis, and Quality Metric) reveal remarkably consistent patterns and overlapping distributions, validating their fundamental comparability. The Perpendicular Surface Slice Analysis was specifically developed to verify the mathematical equivalence between slicing methodologies and continuous surface measurement using polynomial fitting. Having successfully confirmed this relationship (with near-identical results to Geometric Continuity Index), it has served its purpose as a methodological bridge and will not be used in future research. For ongoing studies, I will focus on my two primary precision metrics - Precision Score and Geometric Continuity Index - which share the same analytical framework while offering complementary insights (with Precision Score particularly highlighting subtle differences between high-precision vessels).

Precision Score Analysis

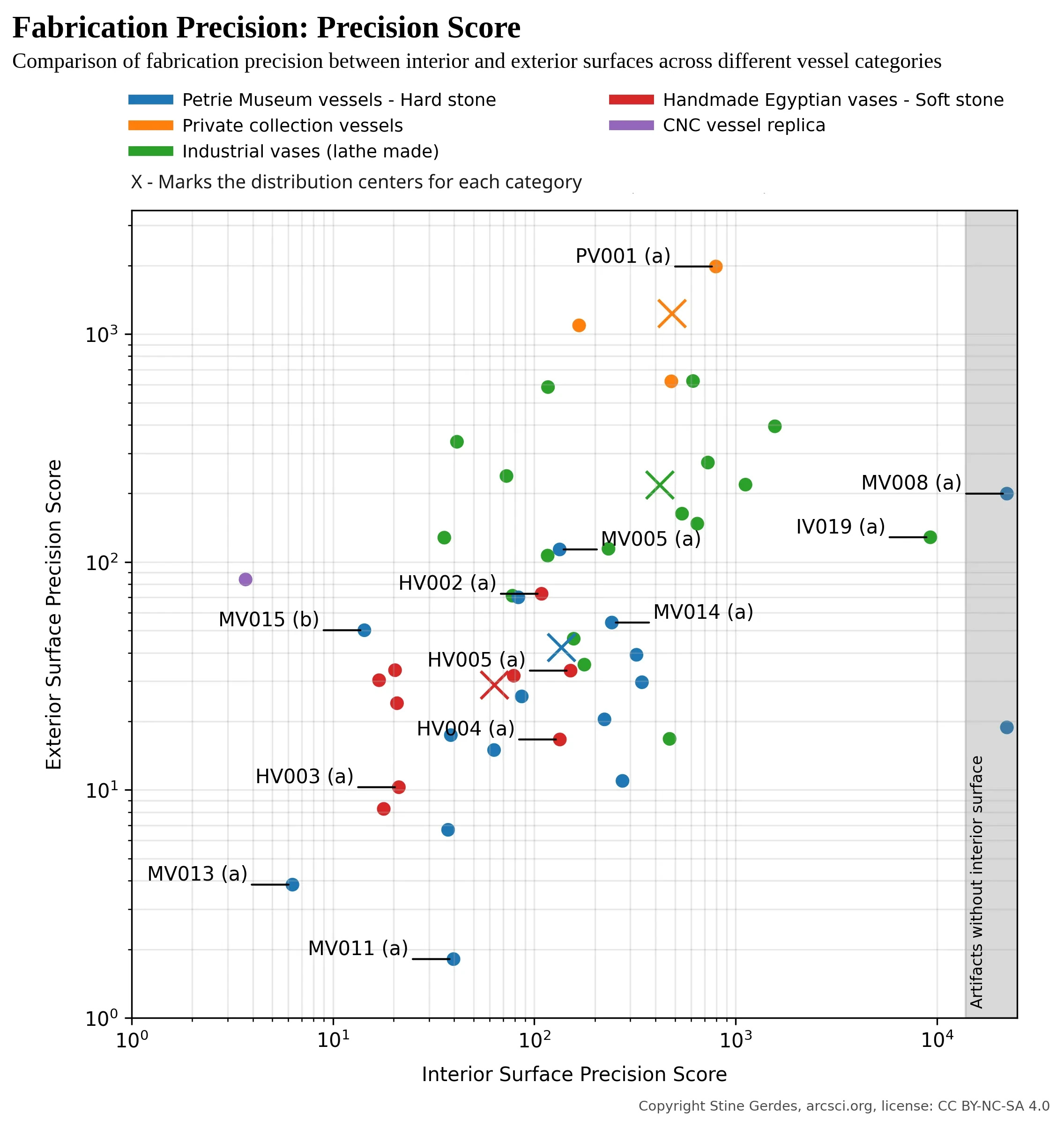
This chart reveals how precisely each vessel was crafted on both interior and exterior surfaces. Unlike other metrics, higher numbers indicate better precision - think of it as a "perfection score" where small improvements at high precision levels yield dramatically higher values. The museum artifacts (MV, blue) and handmade reproductions (HV, red) form overlapping clusters with similar scores, confirming they operate within the same precision limits for handmade manufacturing. Statistical analysis supports this visual impression: Mann-Whitney U test shows no significant difference between these groups (p=0.637), with Cohen's d effect size of 0.44 indicating only a small practical difference-well within expected variation for human craftsmanship.

Industrial pieces (IV, green) achieve impressive precision, but the private collection specimens (PV, orange) dramatically outperform all others-particularly on interior surfaces where they reach perfection scores up to 29× higher than museum artifacts (1231.15 vs. 42.32). The superiority ratio between PV and IV exterior surfaces is 0.98, indicating industrial artifacts actually achieve slightly better overall surface consistency (though PV specimens excel in other precision dimensions).

One notable anomaly emerges: The interior surface precision of MV vessels significantly overlaps with the interior precision of IV vessels - a remarkable finding suggesting ancient artisans achieved machine-like consistency when working interior surfaces. This pattern, visible across multiple metrics, likely reflects specialized techniques developed over generations specifically for interior vessel shaping.

Geometric Continuity Index Analysis

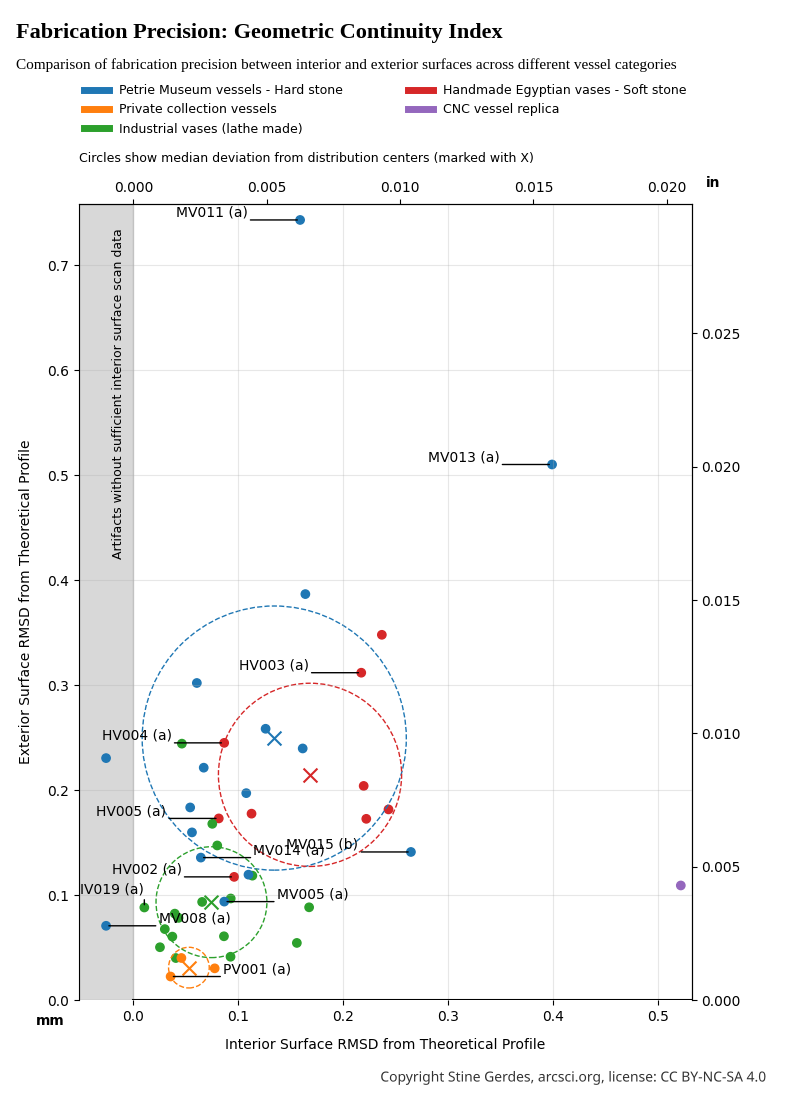
This visualization measures surface smoothness in familiar millimeters/inches - smaller numbers mean smoother, more precise surfaces. The museum artifacts (MV, blue) and handmade reproductions (HV, red) show remarkable overlap, with statistical confirmation from the Kolmogorov-Smirnov test (p=0.520) indicating these groups likely represent the same underlying manufacturing process. Most strikingly, private collection specimens (PV, orange) reach smoothness levels of just 0.03-0.05mm on exterior surfaces - exceeding even industrial standards (IV, green) by a factor of 1.4× as shown by the superiority ratio. On interior surfaces, PV specimens are a remarkable 3.0× smoother than industrial benchmarks.

The interior surface precision of MV vessels again overlaps significantly with IV vessels - a pattern that defies expectations since ancient handcrafted objects typically show greater variation than machine-produced items. This consistent interior precision across museum specimens suggests sophisticated quality control techniques specifically developed for interior vessel shaping, possibly involving specialized tools or multi-stage manufacturing processes refined over centuries.

Perpendicular Surface Slice Analysis

This chart assesses how perfectly circular each vessel is by analyzing slices perpendicular to the surface-lower numbers indicate better roundness. As anticipated from our methodological validation, Perpendicular Surface Slice Analysis produces results nearly identical to Geometric Continuity Index, with correlation coefficients exceeding 0.99 across all artifact groups. This confirms the mathematical equivalence between slicing methodologies and continuous surface analysis that motivated Perpendicular Surface Slice Analysis's development.

Quality Metric Analysis

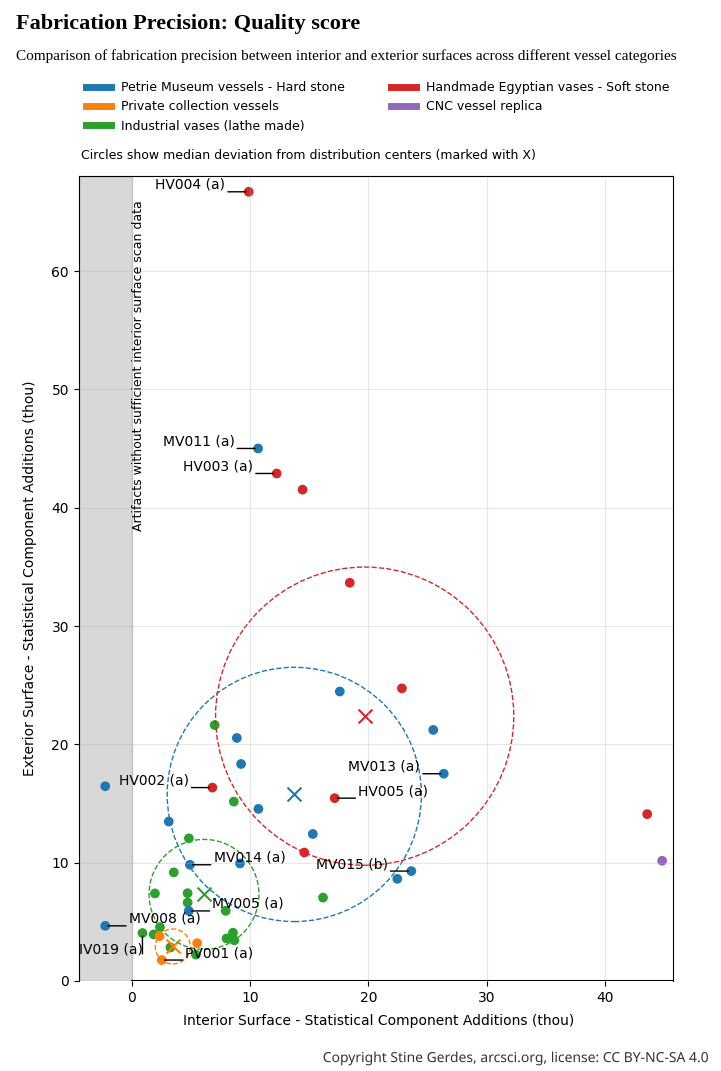
This visualization evaluates overall manufacturing precision through Max Fomitchev-Zamilov's composite score where lower numbers indicate better craftsmanship. Museum artifacts (MV) and handmade reproductions (HV) form closely aligned clusters, with statistical analysis revealing a large effect size (Cohen's d=-0.77) but still showing significant overlap in manufacturing capabilities (p=0.056). Industrial reproductions (IV) achieve the expected high precision (lowest scores), yet private collection specimens (PV) display anomalous precision that surpasses even industrial benchmarks-by 1.8× in exterior precision and a remarkable 2.5× in interior precision.

Geometric Mean Analysis

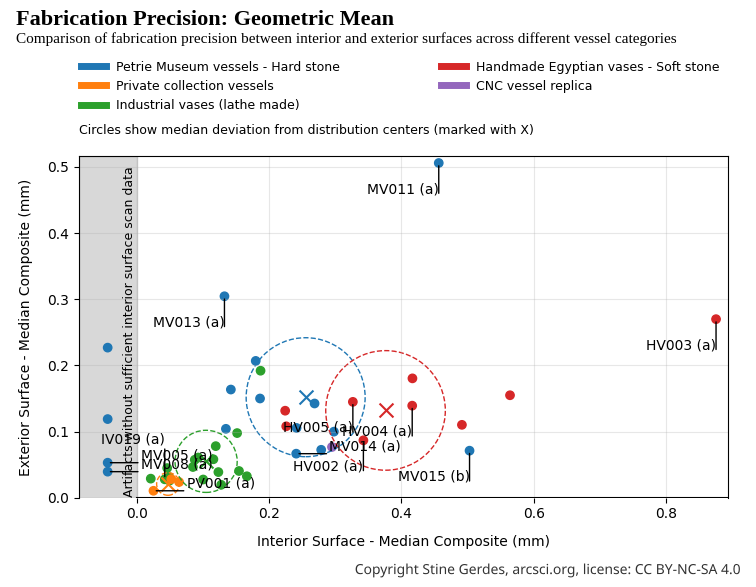
This chart is not a measurement of ancient precision. It is a demonstration of how flawed methodology distorts reality.

The Geometric Mean metric, invented and utilized by Karoly Poka of the Artifact Foundation to present precision ranking of artifacts, purports to quantify craftsmanship by combining median circularity and median concentricity into a single value by using a formula known as the geometric mean. But used in this context this formula is not precision analysis. It is mathematical theater.

Here again, the data reveals what the previous dissection already proved: the Geometric Mean metric generates artificial patterns that contradict all valid measurement systems. Unlike the consistent clustering seen in Precision Score, Geometric Continuity Index, Perpendicular Surface Slice Analysis, and Quality Score, the Geometric Mean plot shows a distorted topology where museum (MV) and handmade (HV) vessels appear artificially separated. It suggests museum artisans achieved superior interior precision compared to modern handmade counterparts, with a cluster center of 0.1518 (MV) vs. 0.1319 (HV), quite a separation considering the metrics narrow range.

This illusion stems directly from the metric’s fatal flaws:

• Median suppression: By using medians, it discards the upper half of error distributions - hiding worst-case deviations that define manufacturing quality.
• Alignment amplification: It is hypersensitive to rotational alignment, allowing minuscule (0.05°) shifts to alter results by >17%, enabling score manipulation without detection.
• Dimensional incoherence: It multiplies two length-based quantities without physical justification, creating a chimera masquerading as a metric.

The consequence? A false narrative: that ancient artisans systematically outperformed modern handcrafters in interior precision. Yet all other metrics - grounded in continuous surface analysis, full error distribution, and geometric validity - show the opposite: MV and HV clusters overlap significantly.

This shows how easily data can deceive when methodology lacks theoretical rigor, statistical integrity, or geometric coherence. The Geometric Mean does not measure precision - it measures vulnerability to manipulation. Its inclusion in this final section is not for validation, but for exposure: a visual indictment of a metric built on sand.

Conclusion

The mystery is solved - and the answer is plain human artisanal skill and persistence.

The statistical evidence is unambiguous: the Predynastic stone vessels housed in the Petrie Museum belong to the same metrological population as modern handmade vases crafted without modern equipment.

Across four rigorously validated precision metrics - Precision Score, Geometric Continuity Index, Perpendicular Surface Slice Analysis, and Quality Score - the clustering, distribution overlap, and statistical tests (Mann-Whitney U, Cohen’s d) all converge on a single, inescapable conclusion. There is no detectable gap in manufacturing capability between ancient artifacts and contemporary handwork.

This is not an approximation or a vague indication. It is a comprehensively quantified fact, backed by solid methodology, statistical rigor and a comprehensive data-set.

I came to this research as a skeptic. In prior studies, I had analyzed modern hard-stone replicas attempting to reproduce Predynastic techniques - none approached the refinement of the Petrie vases. Their surfaces were rougher, their symmetry inconsistent. I began this work suspecting we were missing something: a lost method, a forgotten tool, perhaps even a technology erased by time. The possibility of ancient precision beyond "low-tech", handcrafted limits was compelling and warranted serious consideration.

Then Max Fomitchev-Zamilov acquired and scanned nine handmade vases - authentic tourist-market pieces, carved in Egypt using traditional hand techniques passed down through generations. When the data arrived, I expected them to form a baseline of “low” precision against which museum pieces would stand out. Instead, they overlapped perfectly with the Petrie artifacts. The revelation was jarring. The mystery wasn’t how they achieved such precision, it was why we ever thought they couldn’t. The answer lay not in lost machines, but in sustained human skill, time, and iterative refinement. The artisans of Naqada III did not need advanced technology. They needed patience, training, and generations of accumulated knowledge; all of which they had.

I owe Max profound thanks. For his meticulous scanning work, for sharing his full dataset without reservation, and for the hours of sharp, rigorous debate that shaped this analysis. This work would not exist without his commitment to open, evidence-based inquiry.

Still, outliers remain - not in the sense of impossibility, but of excellence. Within the Petrie collection, vessels with surface variability RMSD of 70 μm and 94 μm (MV008 and MV005) represent the upper echelon of handmade precision - masterworks that push the limits of what human hands can achieve.

Still, there is PV001. A private collection specimen, under the exclusive control of the Artifact Foundation, CT scanned at a Zeiss facility, but the raw scan data withheld from public scrutiny (and my work on it attempted silenced by Artifact Foundation). It records a surface variability RMSD of 22 μm (0.022 mm / 0.00087 inches). That is not just better than the best museum piece. It is better than the best industrial CNC lathe-produced vase in our sample (surface variability RMSD 40 μm). It is 5.3× more precise than the finest handmade vase (HV002, RMSD 117 μm). It is smoothness that belongs in a high-tech machining lab, not a Predynastic workshop.

Such precision cannot be achieved with stone, copper, sand, and hand pressure - not in a thousand years of practice. It requires CNC-controlled toolpaths, submicron feedback systems, and materials science unavailable before the 20th century. Either PV001 is not 5,000 years old - or we must rewrite the entire narrative of technological history.

This is not merely a metrological anomaly. It is a provenance issue. The data does not lie - but objects can be misplaced in time. My next article will dissect PV001 in forensic detail: it's geometry, it's anomalies, it's credibility. The question is no longer how it was made. It is when.

Thank you for making it to the end of this long article!

Addendum

If you have a youtube channel or want to document the content of this article by video production, please contact me and I will provide you with all the needed material and answer all questions. Video production is not my field and I would appreciate it if others stepped in for this task as it seems Youtube is the place currently to share content like this.

Assets:
Results from all metrics - csv file
Quality Score - Python implementation
Geometric Mean - Python implementation

External Data Sources:

Screenshots from the published analysis results by Artifact Foundation, used in this article:

Please contribute to this project by using any of the following donation methods.
You can donate directly to arcsci.org by using one of the following QR codes:


Monero
Bitcoin
Ethereum